Каждый мечтает удвоить или даже утроить свой капитал. Для этого люди приходят на фондовый рынок , покупают акции, облигации и другие активы. Но прежде надо поставить цель и посчитать, через сколько она будет достигнута. Для это и было выработано «правило 72», которое позволяет приблизительно рассчитать, через сколько лет удвоится капитал при заданной ставке.
Перед тем, как мы перейдем к сути правила, разберемся, что такое сложный процент. Сложный процент — это начисление процентов и на основную сумму, и на проценты за предыдущий период. Предположим, вы положили на вклад ₽100 тыс. под 10%. За первый год вы получите ₽10 тыс. На второй год проценты будут начисляться уже на 110 тыс. — доход получится уже 11 тыс., на третий 12,1 тыс. (121 000*10%) и так далее. Итого за три года доход получится ₽33,1. В случае с простыми процентами, доход будет равен лишь 30 тыс.
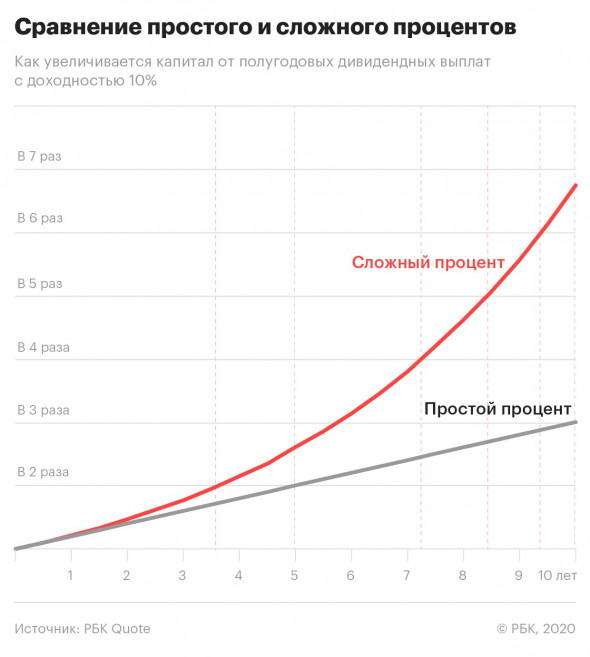
Рассмотрим другой пример, где вы вложили ₽100 тыс. в акцию со стабильной полугодовой дивидендной доходностью 10%. Если вы будете реинвестировать полученные дивиденды , то почувствуете магию сложного процента. Уже через 3,5 года вы почти удвоите свой капитал, а через 10 лет — увеличите его в 6,7 раз. Для сравнения — без реинвестирования капитал за 10 лет лишь утроится. В этом и заключается сила сложного процента.

Этот математический принцип позволяет быстро посчитать приблизительное количество лет, которое потребуется для удвоения капитала при инвестировании под фиксированную ставку сложных процентов. Для этого нужно найти отношение 72 к процентной ставке. К примеру, вы удвоите свой капитал за 4 года, если вложите средства под 18% годовых (72 / 18 = 4).
Первое упоминание о «правиле 72» приписывают Луке Пачоли, известному итальянскому математику. Он описал эту закономерность в своей книге 1494 года «Сумма арифметики, геометрии, пропорции и пропорциональности», не указав, как именно было выведено число 72.
На самом деле, такое соотношение, которое показывает необходимое количество лет для удвоения капитала при фиксированной ставке, можно легко вывести из формулы сложных процентов. Однако если рассчитывать, то получится не 72, а 69,3. Но математики стали использовать 72, так как оно близко по значению к 69,3, а главное — имеет больше делителей (2, 3, 4, 6, 12 и так далее), что дает простоту в расчетах.
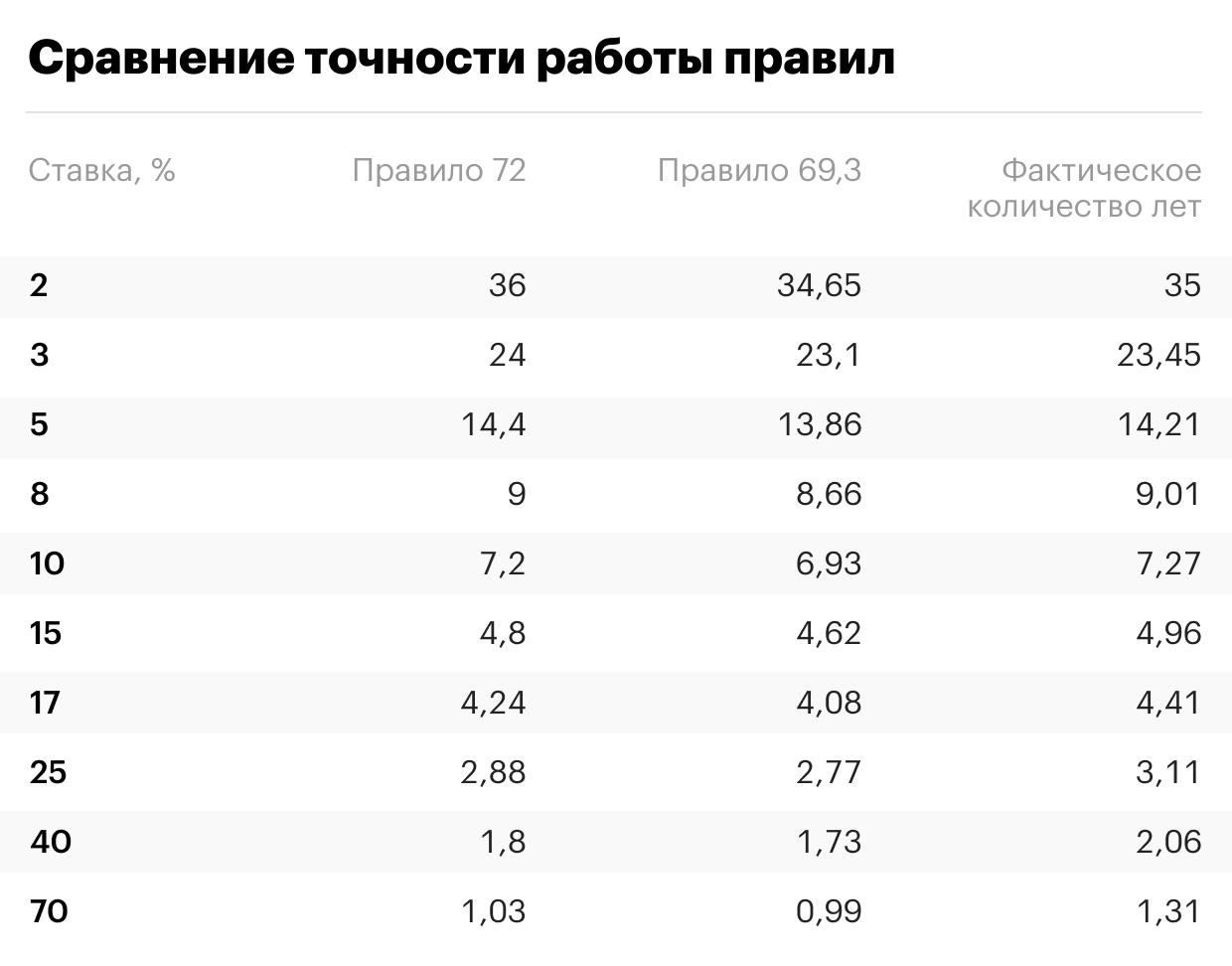
Это правило хорошо работает с процентными ставками в диапазоне от 6% до 10%. Однако при увеличении ставки погрешность увеличивается. Экономисты советуют прибавлять единицу к 72 при каждом отклонении на три процентных пункта от 8% (середина идеального диапазона «правила 72»). К примеру, если рассчитываете правило для 11%, то в числитель следует ставить 73, если 14%, то 74, и по аналогии.
Также это правило работает, если вы хотите посчитать, под сколько процентов надо инвестировать средства, чтобы удвоить капитал через n лет. Например, если вы хотите удвоить капитал через 6 лет, то вам нужно проинвестировать деньги под 12% годовых (72 / 6 = 12). Формула остается прежней, но теперь в знаменателе будет количество лет.

Следует помнить, что все расчеты приблизительны и для точности все же необходимо воспользоваться формулой. Но описанное правило позволит легко прикинуть нужное количество лет.
Естественно, что на фондовом рынке нет никаких гарантий доходности, тем более стабильной (кроме облигаций). Но если использовать среднюю доходность какого-либо индекса за определенный период, то можно оценить будущую выгоду.
Например, среднегодовая доходность с 1993 года ETF -фонда SPDR S&P 500 Trust (тикер SPY), который наиболее точно повторяет динамику индекса S&P 500, составляет 10,48%. Тогда мы можем посчитать, за сколько лет удвоится наш капитал при инвестировании в этот ETF-фонд. При делении 72 на 10,48 получим, что нам понадобится около 7 лет для удвоения капитала при инвестировании в S&P 500.

